Про форматы чисел с плавающей точкой, познавательное
"FP64, FP32, FP16, BFloat16, TF32, and other members of the Zoo"
Библиотека Си++, реализующая плавающие числа с произвольным размером экспоненты и мантиссы: https://github.com/oprecomp/FloatX
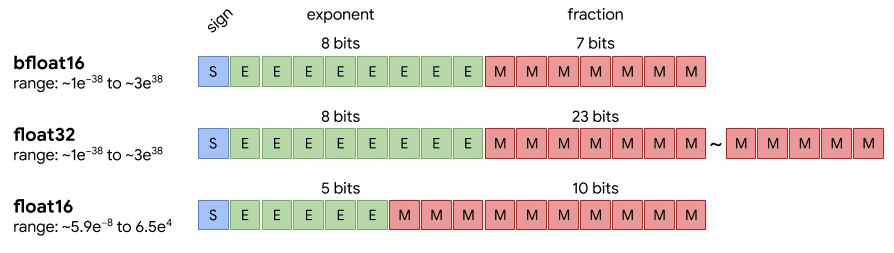
К примеру, BFloat16 реализуется как тип float<8,7>. Размер экспоненты равен 8, размер мантиссы - 7.
Библиотека Си++, реализующая плавающие числа с произвольным размером экспоненты и мантиссы: https://github.com/oprecomp/FloatX
К примеру, BFloat16 реализуется как тип float<8,7>. Размер экспоненты равен 8, размер мантиссы - 7.

no subject
Для всякого машинного лернинга годится или bfloat16, или вообще сразу брать логарифмы и не мучаться. (Я когда-то сразу в логарифмы перегонял, все равно на больших данных будут большие числа.)
no subject
Для inference массово используется традиционный int8. На плавающей точке страшно неэффективно выходит. С переходом на int8 вылазит проблема quantization и потери точности. Чтобы не париться с квантованием, народ пробует BF16, но опять же преимущества пока непонятны.
no subject
no subject
или bfloat16, или float16 - зависит от того, хватит ли пяти бит для порядка (вряд ли)
no subject
Во-первых, тот же размер экспоненты, что у традиционного float32. То есть одним махом избавляемся от проблемы quantization. Тренируем сетку как обычно на fp32, а потом просто укорачиваем мантиссы.
Во-вторых, тот же размер мантиссы, что у int8. То есть в хардвере можно использовать те же умножители, что и для классического целочисленного inference.
no subject
no subject
Вот статья: https://pdfs.semanticscholar.org/da1f/299a7149b98c50b508a1c9886ff3d01b0233.pdf
Но суть не в экономии битов, а в проблеме quantization, которую приходится решать, если мы уменьшаем экспоненту. А решать её трудно и дорого, часто ценой retraining.
no subject